Identification methods for experimental vibration analysis
GOALS OF THE RESEARCH
In the virtual prototyping era, experimental vibration testing still plays a crucial role during the certification of an engineering product. However, as many industries face increasing technological, economic and environmental pressures, the need to embrace nonlinear dynamical behavior mounts further. We are currently at a stage where practising engineers, who were used to ignore or avoid nonlinearity during design and testing, are now looking for the next generation of experimental vibration analysis techniques. In this context, the objective of this doctoral project is to develop novel testing methodologies and algorithms that can rigorously and effectively characterize the dynamics of a structure exhibiting nonlinearities.
STATE OF THE ART
Experimental vibration analysis amounts to identifying the frequency response functions (FRFs) and modal parameters, namely mode shapes, resonance frequencies and damping ratios, directly from experimental data. The techniques available today, packaged in software commercialized by, e.g., Siemens and Bruel & Kjaer, are really quite sophisticated and advanced. In aerospace engineering, broadband and swept-sine forcing is classically applied during aircraft/spacecraft ground vibration tests in order to identify FRFs and modal parameters. One inherent assumption of classical experimental vibration analysis is linear structural behavior. However, with the continual interest in expanding the performance envelope of engineering systems, nonlinearities are more and more often encountered. For instance, vibration testing of two aircraft of the Airbus family, namely the A400M and the A350XWB, revealed nonlinearities in elastomeric engine mounts and hydraulic actuators [1], in landing gears [2] and in the auxiliary power unit of the airframe tail-cone [3]. Satellites are other examples of aerospace applications where nonlinearity may significantly impact the dynamics behavior [4].
The increasing manifestations of nonlinearity have motivated researchers to develop rigorous nonlinear extensions of FRFs and modal parameters, termed nonlinear frequency response functions (NLFRFs) and nonlinear normal modes (NNMs), respectively. There now exist relatively robust numerical techniques to compute NLFRFs and NNMs from finite element models. We note that the Space Structures and Systems Laboratory (S3L) is recognized as a leading contributor in this area, see, e.g., [5-6]. However, these generalizations come at a price. In view of the absence of superposition principle, nonlinear systems exhibit dynamical phenomena with no linear counterparts including sub- and superharmonic resonances, modal interactions, quasiperiodic oscillations, bifurcations and chaos. For illustration, Figure 1 compares the NLFRFs of an Airbus Defense and Space spacecraft in linear-like and nonlinear regimes of motion.
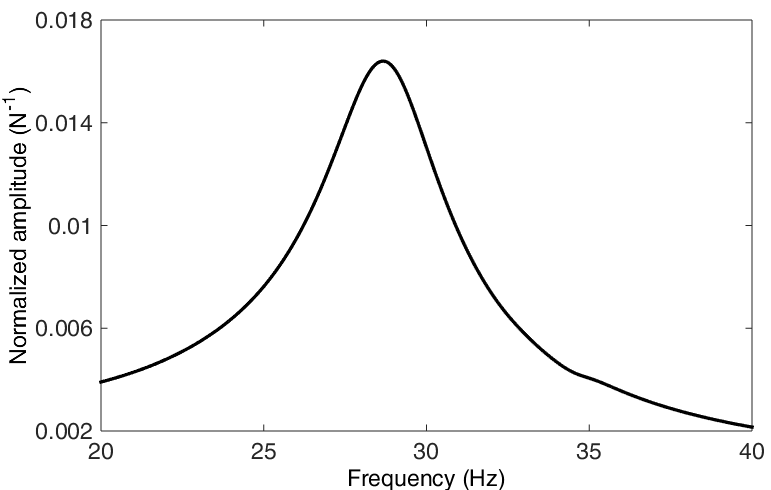
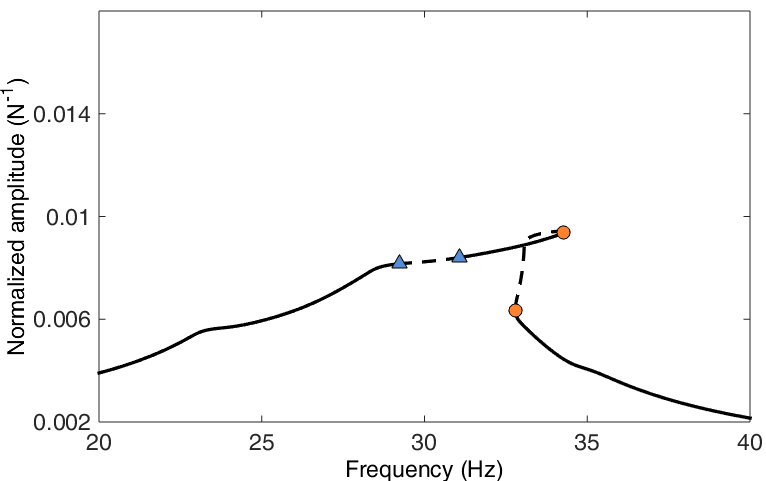
Figure 1: NLFRFs of a satellite with a nonlinear vibration isolation device [6]. The NLFRFs are calculated numerically from a finite element model. Left: NLFRF in a linear-like regime (low forcing level); right: NLFRF in a nonlinear regime (high forcing level). Several bifurcations change the stability and introduce new branches (not displayed here). The comparison of these two figures illustrates the important complexity introduced by nonlinearity.
Despite the recent progress in nonlinear simulation, the identification of NLFRFs and NNMs from experimental data remains an extremely challenging exercise. Indeed, identifying the variety of new nonlinear phenomena using existing linear identification techniques is bound to failure. Only a few attempts have been achieved to develop adequate identification methods for NLFRFs and NNMs [7-10], but they identify one structural resonance at a time and cannot perform a complete characterization (in terms of bifurcations and stability) of these nonlinear features. A rigorous and complete framework for experimental vibration analysis of nonlinear systems is thus clearly missing in the existing body of knowledge.
OFFLINE IDENTIFICATION METHODOLOGY
The first endeavor of this research is to establish a so-called offline methodology for experimental nonlinear vibration analysis. Specifically, input and output vibration data measured through force and acceleration sensors are collected and processed a posteriori for identifying the NLFRFs. The proposed method relies on the successful integration of two building blocks developed by S3L, namely the frequency-domain nonlinear subspace identification (FNSI) method [11] and a harmonic balance-based continuation method [6]. The complete methodology, presented in Figure 2, comprises two main steps. First, following the broadband excitation of the system of interest, the FNSI method is exploited to derive a state-space model of the system. The key advantage is that this model is purely experimental, i.e., it does not require the existence of a finite element model. The identified model, expressed in discrete time to ensure proper numerical conditioning and fast time-domain simulations, is subsequently used in conjunction with the multiharmonic balance method. To do so, the input, state and output vectors of the model are expanded in truncated Fourier series, and the resulting amplitude equations are solved using Newton-Raphson iterations. Eventually, the association of multiharmonic balance with a pseudo-arclength continuation algorithm allows for the NLFRFs together with their bifurcations.
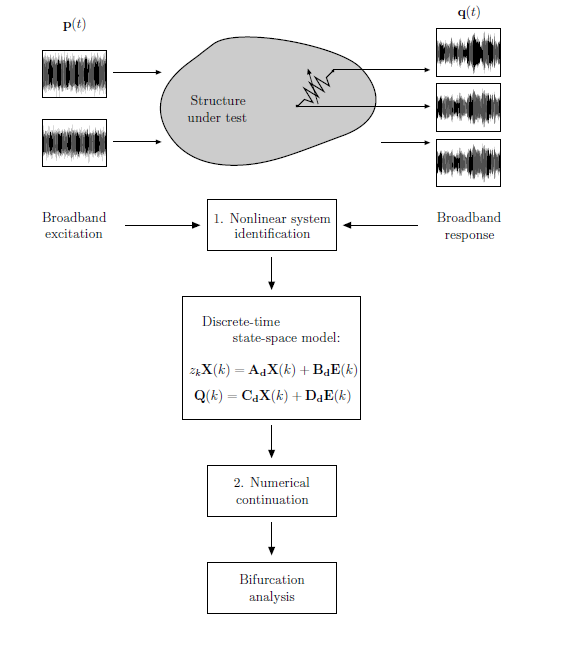
Figure 2: Proposed offline identification methodology.
ONLINE IDENTIFICATION METHODOLOGY
The second important contribution of this doctoral work is to exploit the completely new testing philosophy relying on control-based continuation (CBC) [13]. CBC is an extension of classical numerical continuation to physical experiments which does not require a mathematical model. As shown in Figure 3, it combines stabilizing, non-invasive feedback control and path following techniques to follow experimentally the evolution of the steady-state response of a system as the forcing frequency or forcing amplitude is varied. The presence of the controller is advantageous because both the stable and the unstable parts of the NLFRFs can be identified; bifurcations can also be uncovered and classified experimentally. Even though the continuation cannot be achieved in real time, the NLFRFs are obtained online without the need for further postprocessing.
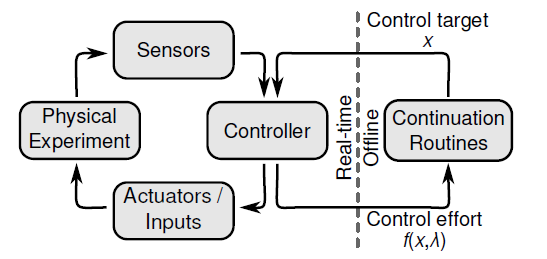
Figure 3: Schematic overview of an experimental set-up for control-based continuation.
CBC is still in its infancy. It was applied to very low-dimensional systems [14,15] and has not yet been used to fully characterize the different bifurcations of an engineering structure. Thus, the present proposal seeks to address the application of CBC to more realistic structures (for which noise is inevitable present) and to structures exhibiting different families of bifurcations including fold or saddle-node bifurcations, branch point bifurcations and Neimark-Sacker bifurcations. The existing CBC algorithms will thus have to be “robustified” and generalized. An additional originality of our research work will be to use CBC to detect isolated resonance curves, which are resonance curves detached from the main NLFRF. This dynamical phenomenon is still largely ignored in the technical literature, but it can be observed even for realistic structures [6].
NUMERICAL AND EXPERIMENTAL VALIDATION
To validate the two developed approaches, numerical simulations will be performed using low- and high-dimensional structural examples, e.g., with the nonlinear finite element model of a full-scale satellite that we have at our disposal. In parallel, an experimental demonstration using the S3L set-up in Figure 4 will be carried out. The system, comprising two degrees of freedom and two nonlinear springs, exhibits complex nonlinear dynamics including fold, Neimark-Sacker bifurcations, modal interactions and isolated resonances. Another interesting feature of this test rig is that it is fully tunable, i.e., linear and nonlinear springs can be removed easily and the corresponding coefficients can be modified.

Figure 4: S3L set-up with two masses interconnected with linear and nonlinear springs. Although seemingly simple, it exhibits complex nonlinear phenomena.
REFERENCES
[1] J.R. Ahlquist et al., Assessment of nonlinear structural response in A400M GVT, Proceedings of the 28th International Modal Analysis Conference (IMAC), Jacksonville, USA, 2010.
[2] P. Lubrina et al., AIRBUS A350 XWB GVT: State-of-the-art techniques to perform a faster and better GVT campaign, Proceedings of the 32nd International Modal Analysis Conference (IMAC), Orlando, USA, 2014.
[3] E. Menga et al., Nonlinear dynamic analysis of assembled aircraft structures with concentrated nonlinearities, Proceedings of the 16th International Forum on Aeroelasticity and Structural Dynamics (IFASD), Saint Petersburg, Russia, 2015.
[4] J.P. Noel, L. Renson, G. Kerschen, Complex dynamics of a nonlinear aerospace structure, Journal of Sound and Vibration 333, 2588-2607, 2014.
[5] G. Kerschen, M. Peeters, J.C. Golinval, C. Stephan, Nonlinear modal analysis of a full-scale aircraft, AIAA Journal of Aircraft 50, 1409-1419, 2013.
[6] T. Detroux, L. Renson, L. Masset, G. Kerschen, The harmonic balance method for bifurcation analysis of large-scale nonlinear mechanical systems, Computer Methods in Applied Mechanics and Engineering 296, 18-38, 2015.
[7] M.F. Platten, J.R. Wright, G. Dimitriadis, J.E. Cooper, Identification of multi-degree of freedom non-linear system using an extended modal space model, MSSP 23, 8-29, 2009.
[8] A. Carrella, D.J. Ewins, Identifying and quantifying structural nonlinearities in engineering applications from measured FRFs, MSSP 25, 1011-1027, 2011
[9] M. Peeters, G. Kerschen, J.C. Golinval, Modal testing of nonlinear vibrating structures based on nonlinear normal modes: experimental demonstration, MSSP 25, 1227-1247, 2011.
[10] S. Peter, R. Leine, Excitation power quantities in phase resonance testing of nonlinear systems with phase-locked-loop excitation, MSSP 96, 139-158, 2017.
[11] J.P. Noel, G. Kerschen, Frequency-domain subspace identification for nonlinear mechanical systems, MSSP 40, 701-717, 2013.
[12] T. Dossogne, J.P. Noël, C. Grappasonni, G. Kerschen, B. Peeters, J. Debille, M. Vaes, J. Schoukens, Nonlinear ground vibration identification of an F-16 aircraft, International Forum on Aeroelasticity and Structural Dynamics, Saint-Petersbourg, Russia (2015).
[13] J. Sieber et al., Experimental continuation of periodic orbits through a fold, Physical Review Letters 100, 2008, 244101.
[14] E. Bureau, F. Schilder, M. Elmegard, I.F. Santos et al., Experimental bifurcation analysis of an impact oscillator – Determining stability, Journal of Sound and Vibration 333, 2014, 5464-5474.
[15] L. Renson, A. Gonzalez-Buelga, D.A.W. Barton, S.A. Neild, Robust identification of backbone curves using control-based continuation, Journal of Sound and Vibration 367, 2016, 145-158.



